滚动轴承故障信号处理处理方法有哪些？

1.有效值和峰值

不光滑滚动轴承的振动瞬时值是随时间变化而变化，作 为表示这种变化大小的方法,有效值有着广泛使用的价值。

有效值也称作平均有效值。有效值对表面皱裂均匀磨损那样 无规则振动波形可以给出恰当的评价。

对于表面剥落、碎裂、压痕那样具有瞬态变化的冲击振 动,峰值比有效值适用。其原因是由于冲击波峰的振幅大， 峰的持续时间短，用有效值评价，由于需要进行时间平均, 其检测能力是很低的。

峰值是在某个时间内表示出来的振幅 的最大值。对瞬时现象可得出正确的指示值。对初期阶段的 表面裂纹、剥落非常容易检测出来。

不过由于响应敏感，在 受外界干扰情况下，会使测定值变动很大。

2.波峰系数

波峰系数是指峰值与有效值之比。正弦波的波峰系数是 V2 ,滚动轴承正常时波峰系数是4~5,当滚动轴承出现剥 落、裂纹、碎裂时，波峰系数达10以上。

波峰系数不受滚动轴承的尺寸、转速、载荷的影响，判断轴承故障可非常单纯 地进行。波峰系数还不受振动绝对水平所支配，所以检测系 统的灵敏度和放大率即便有变化，也不会出现误差。

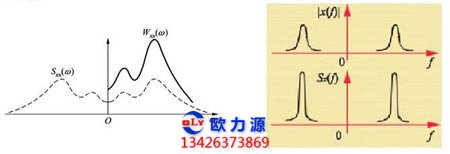
3.包络线检波信号的频率分析

对于轴承表面剥落产生的冲击脉冲振动波形用包络线检 波来分析是有效的。

从表面频谱图米看,振动时间波通过加包 络线检波器检波后，振动时域波变成了包络线波形。通过对 所获得的包络线波形进行频谱分析，就得到了包络线的频谱。

从频谱图上得知最大振幅对应的频率是多少，,再与故障轴承各元件故障频率进行比较，很容易知道剥落处在那个元 件上。

此方法能将外界干扰和其它异常信号分离出去,这是 包络线检波信号频谱分析的最大优点。

4.同周期相加分析

同周期相加分析是在有因剥落等引起冲击振动间隔发生 的周期性情况下使用。

其效果与频率分析一样。它也称平均 应答分析。在剥落引起冲击振动的发生间隔中，将同期振动 信号分段，并将其重合一个一个地加在一起，这是把异常的 振动信号强调出来的一种方法。

由于剥落产生的冲击振动经 常在相同的位置上相加，随着相加次数增多,就增加了异常 信号的强调效果。

反之，外界干扰的非同周期振动,在无规 则的位置相加，其强调程度总比前者低，因此突出了故障频 率成分，便于分析。

注意的是: 在相加时，如冲击振动的相位稍微错位(即不 是完全同周期) 因波形正负抵消就失去相加的效果。因此在进 行同周期相加分析时有必要对振动信号施行绝对值检波。

5.振幅的概率密度函数

概率密度函数是着眼于在振动的振幅轴上的分析方法。

正常滚动轴承概率分布窄,剥落产生时,分布广。从概 率密度分布的形状可进行故障诊断。然而还需加以定量 把概率密度分化，布广的幅值用量表示出来。这个量的 大小可由陡度来反映。

轴承振动的概率密度分布， 波峰系数,与振幅的概率密度函数的共同缺点是对表面 皱裂形式的失效很难确诊正确或是异常。